Gráficos tridimensionales

Curvas tridimensionales

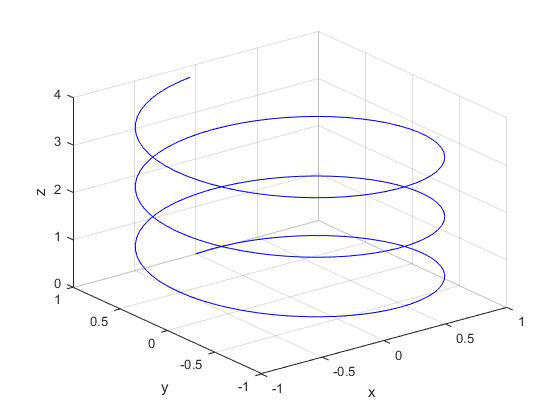
El caso más sencillo se presenta cuando x, y y z son funciones de un parámetro t. Utilizamos el comando plot3 para dibujar la línea tridimensional.

x=sin(t)
y=cos(t)
z=0.2·t

t=0:0.1:6*pi;
x=sin(t);
y=cos(t);
z=0.2*t;
plot3(x,y,z,'b')
grid on
xlabel('x'); ylabel('y'); zlabel('z')

Superficies tridimensionales

Algo más complicado es mostrar una superficie tridimensional descrita por una función de dos variables z=f(x,y)

El primer paso es crear una rejilla en el plano XY que cubra el dominio de la función y el segundo paso consiste en el cálculo del valor de z para cada uno de los puntos de la rejilla.

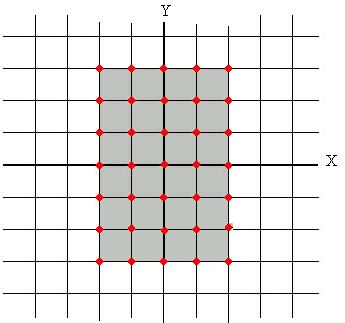
En la figura se muestra el conjunto de puntos del plano XY para el dominio -2≤x≤3, -1≤y≤3 con espaciado de una unidad. Los puntos de la rejilla se definen mediante dos matrices. La matriz X guarda las abscisas de los puntos y la matriz Y las ordendas de dichos puntos. La función meshgrid de MATLAB crea la matriz X y la matriz Y.

>> x=-2:2;
>> y=-3:3;
>> [X,Y]=meshgrid(x,y)
X =
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
Y =
    -3    -3    -3    -3    -3
    -2    -2    -2    -2    -2
    -1    -1    -1    -1    -1
     0     0     0     0     0
     1     1     1     1     1
     2     2     2     2     2
     3     3     3     3     3

Se calculan los valores de z=f(x,y) para cada unos de los puntos de la rejilla. En este caso z=x²-y²

>> Z=X.^2-Y.^2
Z =
    -5    -8    -9    -8    -5
     0    -3    -4    -3     0
     3     0    -1     0     3
     4     1     0     1     4
     3     0    -1     0     3
     0    -3    -4    -3     0
    -5    -8    -9    -8    -5

Incrementamos la resolución y dibujamos la superficie mediante la función mesh,

x=-2:0.1:2;
y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.^2-Y.^2;
mesh(X,Y,Z);
xlabel('X')
ylabel('Y')
zlabel('Z')

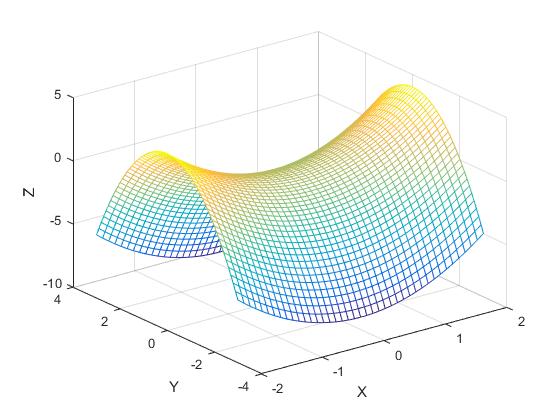
Alternativamente, podemos dibujar la misma superficie utilizando la función surf.

Vamos a dibujar la función

$z = \frac{\sin r}{r} r = \sqrt{x^{2} + y^{2}}$

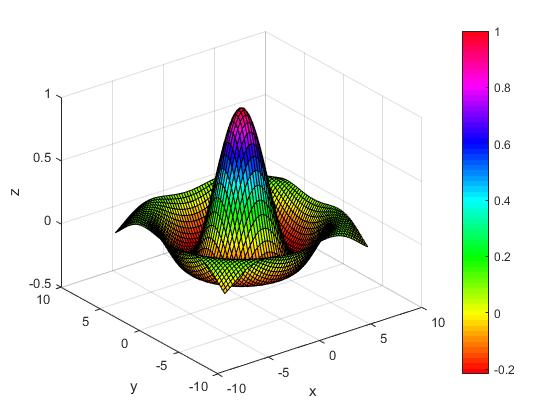
en el dominio el dominio -7≤x≤7, -7≤y≤7 con espaciado de 0.25. Evitamos a indeterminación 0/0 en el origen sumando eps a r.

El color de cada elemento de superficie está determinado por el valor de z y el mapa de colores (una lista ordenda de colores)

[x,y] = meshgrid(-7:0.25:7);
r = sqrt(x.^2 + y.^2) + eps;
z = sin(r)./r;
surf(x,y,z)
colormap hsv
colorbar
xlabel('x'); ylabel('y'); zlabel('z')

Superficies definidas de forma paramétrica

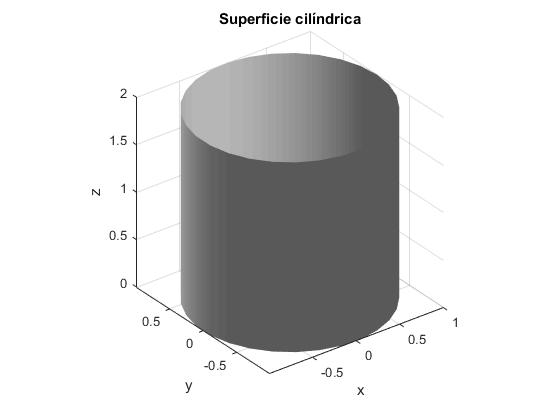
Cilindro

r=1*ones(30,1);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=repmat(linspace(0,2,30),30,1);
surfl(x,y,z);
shading interp
colormap(gray);

axis equal
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cilíndrica')

Cono

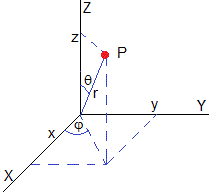
Coordenadas esféricas

x=r·cosφ·sinθ
y=r·sinφ·sinθ
z=r·cosθ

donde 0≤r≤1, 0≤φ≤2π, 0≤θ≤π/2

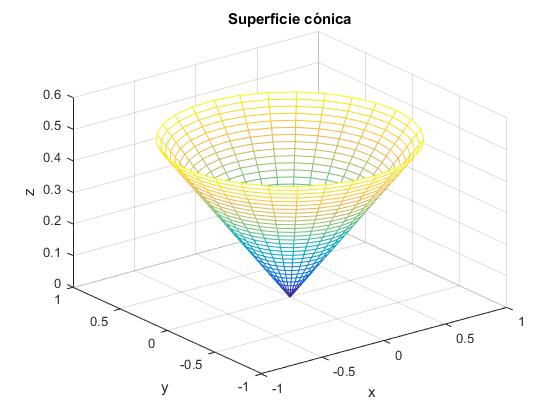
La superficie cónica se define para un valor θ fijo

theta=pi/3;
r=linspace(0,1,30);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
mesh(x,y,z)
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cónica')

Esfera

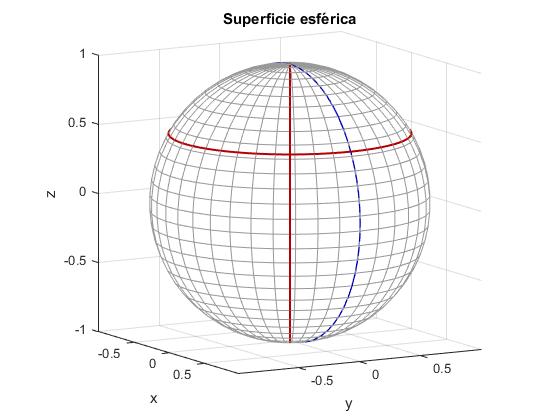
Dibujamos una superficie esférica, y sobre ella el punto P de coordenadas φ y θ

%esfera
R=1;
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6]);
%probar una superficie esférica semitransparente
%set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5) 

%paralelo
theta=pi/3;
phi=0:0.1:2*pi+0.1;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta)*ones(1,length(x));
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
%meridiano de referencia
phi=0;
theta=-pi:0.1:pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
set(h1,'Color',[0,0,.7],'LineWidth',1)
%meridiano
phi=-pi/6;
theta=-pi:0.1:pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)

axis equal
view(60,10)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie esférica')

Superficies de revolución

Al girar alrededor del eje Z la función z=f(x), obtenemos una superficie de revolución

La energía potencial de una masa puntual situada en el origen es E_p(r)=-k/r. Su representación en el plano es

z=@(x) -1./abs(x);
hold on
fplot(z,[1,5],'b')
fplot(z,[-5,-1],'b')
line([0,0],[-0.2,-1], 'lineStyle','--','color','k','lineWidth',1.5)
hold off
grid on
xlabel('x')
ylabel('z')
title('Superficies de revolución')

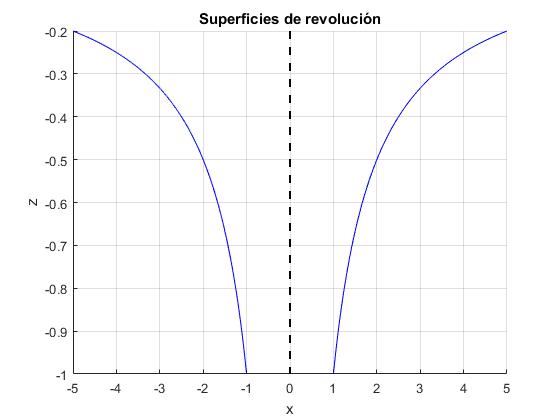
Al girar las gráficas (en color azul) alrededor del eje vertical Z, marcado por la línea a trazos, obtenemos una superficie de revolución. Utilizamos la función cylinder de MATLAB

x=linspace(1, 5, 50);
z=1./x; 
[X,Y,Z]=cylinder(z);
mesh(X,Y,-Z);
xlabel('X'); ylabel('Y'); zlabel('Z') 
title('Superficies de revolución')
view(110,68)

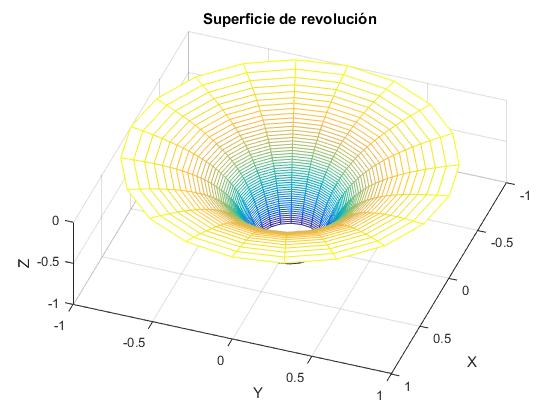
Otra forma de vusualizar la superficie de revolución sin utilizar la función cylinder

r=linspace(1,5,50);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=1./r;

surfl(x,y,-z)
shading interp
colormap(gray);
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficies de revolución')
view(110,68)

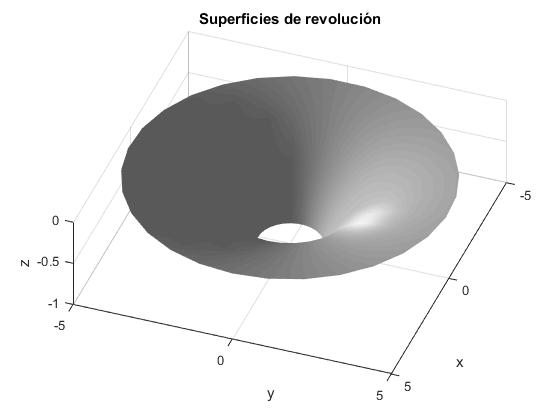
Ejemplos

1.-Tiro parabólico 3D

Se dispara un proyectil con velocidad de 60 m/s haciendo un ángulo de 30°, desde la ventana del vagón de un tren en movimiento a lo largo del eje X con velocidad de 20 m/s. Tómese g=10 m/s²

Calcular la altura máxima y las coordendas (x,y) del punto de impacto.
Representar la trayectoria del proyectil

Ecuaciones del movimiento

${\begin{cases} a_{x} = 0 \\ a_{y} = 0 \\ a_{z} = - 10 \end{cases} {\begin{cases} v_{x} = 20 \\ v_{y} = 30 \sqrt{3} \\ v_{z} = 30 - 10 \cdot t \end{cases} {\begin{cases} x = 20 t \\ y = 30 \sqrt{3} \cdot t \\ z = 30 \cdot t - 5 \cdot t^{2} \end{cases}$

El proyectil alcanza la máxima altura cuando v_z=0, en el instante t=3 s, la altura es de z_max=45 m.

El proyectil impacta contra el suelo cuando z=0, en el instante t=6 s. En este instante las coordenadas del punto de impacto son: x=120 m, y=311.8 m

t=linspace(0,6,50);
z=30*t-5*t.^2;
y=30*sqrt(3)*t;
x=20*t;
plot3(x,y,z)
grid on
axis([0 150 0 350 0 50])
xlabel('x (m)'); ylabel('y (m)'); zlabel('z (m)')

Utilizar la herramienta Rotate 3D del menú Figure Window para cambiar el ángulo de visualización de la parábola.

2.-Dibujar al función

$\begin{array}{l} z = \frac{x y^{2}}{x^{2} + y^{2}} \\ - 1 \leq x \leq 3 1 \leq y \leq 4 \end{array}$

x=-1:0.1:3;
y=1:0.1:4;
[X,Y]=meshgrid(x,y);
Z=(X.*Y.^2)./(X.^2+Y.^2);
mesh(X,Y,Z);
xlabel('X')
ylabel('Y')
zlabel('Z')

3.- Dibujar la función

$\begin{array}{l} z = r θ \\ 0 \leq θ \leq 360 0 \leq r \leq 2 \end{array}$

Utilizar la función pol2cart para convertir coordenadas polares a coordenadas rectangulares.

r=0:0.1:2;
angulo=(0:5:360)*pi/180;
[Ang,Radio]=meshgrid(angulo,r);
Z=Radio.*Ang;
[X,Y] = pol2cart(Ang,Radio);
mesh(X,Y,Z)

Ejemplos en el curso de Física

Movimiento relativo de rotación uniforme

Modos de vibración de una membrana rectangular

Modos de vibración de una membrana circular

Posición del Sol en el Sistema de Referencia Local