Números de Fibonacci

Es la sucesión de números

f₀=0, f₁=1, f₂=1, f₃=2, f₄=3, f₅=5, f₆=8, f₇=13, f₈=21...

Los dos primeros números son el 0 y el 1. El tercero f₂, se obtiene sumando el primero y segundo. El cuarto f₃, se obtiene sumando el segundo y tercero y así, sucesivamente.

f_n=f_n-1+f_n-2, n=2,3,4,...

Podemos crear un función fibonacci recursiva del siguiente modo

function y=fibonacci(n)
    if n==0
        y=0;
    elseif n==1
        y=1
    else
        y=fibonacci(n-1)+fibonacci(n-2);
    end
end

Probamos la función fibonacci en la ventana de comandos para calcular el término 8 de la sucesión

>> fibonacci(8)
ans = 21

Creamos una versión que devuelve la serie de números de Fibonacci f₀, f₁, ...f_n

function Y=fibonacci_1(n)
    Y=[0,ones(1,n)];
    for i=3:n+1
        Y(i)=Y(i-1)+Y(i-2);
    end
end

>> fibonacci_1(8)
ans =     0     1     1     2     3     5     8    13    21

Factorial de un número

Definiremos una nueva versión de la función que calcula el factorial de un número n, n!, que denominaremos, factorial_r.

n!=n·(n-1)·(n-2)...3·2·1

function res=factorial_r(n)
    if n==0
        res=1;
    else
        res=n*factorial_r(n-1);
    end
end

Probamos la función factorial_r en la ventana de comandos para calcular el factorial de 4, 4!, será

>> factorial_r(4)
ans = 24 

Polinomios de Hermite

Los primeros seis polinomios de Hermite son los siguientes.

H₀(x)=1
H₁(x)=2x
H₂(x)=4x²-2
H₃(x)=8x³-12x
H₄(x)=16x⁴-48x²+12
H₅(x)=32x⁵-160x³+120x

Todos los polinomios de Hermite de orden n>2 se pueden expresar en términos de los dos primeros polinomios H₀(x) y H₁(x), de orden cero y uno respectivamente, mediante la siguiente relación de recurrencia.

${\displaystyle H_n(x)=2x·H_{n-1}(x)-2(n-1)H_{n-2}(x)}$

El código de la función recursiva hermite que calcula los valores del polinomio H_n(x) es muy simple. A dicha función se le pasa el orden n del polinomio de Hermite y la abscisa x y devuelve el resultado del cálculo.

function res=hermite(n, x)
    if n==0
        res=1;
    elseif n==1
        res=2*x;
    else
        res=2*x*hermite(n-1,x)-2*(n-1)*hermite(n-2,x);
    end
end

Probamos la función hermite en la ventana de comandos para calcular H₅(2)

>> hermite(5,2)
ans = -16

Triángulo de Pascal

El triángulo de Pascal es una disposición de números tales que cada fila corresponde a los coeficientes del binomio (a+b)^m. Por ejemplo la fila 3 es (a+b)³=1a³+3a²b+3ab²+1b³

Como podemos apreciar la fila m, se puede obtener a partir de la fila m-1, observando que R_m(i)=R_m-1(i-1)+R_m-1(i), para i=2,....m. Con R_m(1)=1 y R_m(m+1)=1

function Y =pascal(m)
    if m==1
        Y=[1,1];
    else
        Y=pascal(m-1);
        A=zeros(1,m-1);
        for i=1:m-1
            A(i)=Y(i)+Y(i+1);
        end
        Y=[1,A,1];
    end
end

>> pascal(5)
ans =     1     5    10    10     5     1

El número π

Para calcular la longitud de una circunferencia, comenzamos con el perímetro de un cuadrado, después con un octógono, un polígono regular de 16 lados y así, sucesivamente

En la figura se muestra un polígono regular de ocho lados

n=2^3; %ocho lados
x0=cos(pi/n);
y0=sin(pi/n);
for i=1:n
    x1=cos(pi/n+2*i*pi/n);
    y1=sin(pi/n+2*i*pi/n);
    line([x0,x1],[y0,y1])
    x0=x1; y0=y1;
end
axis equal
grid on
ylim([-1.1,1.1])

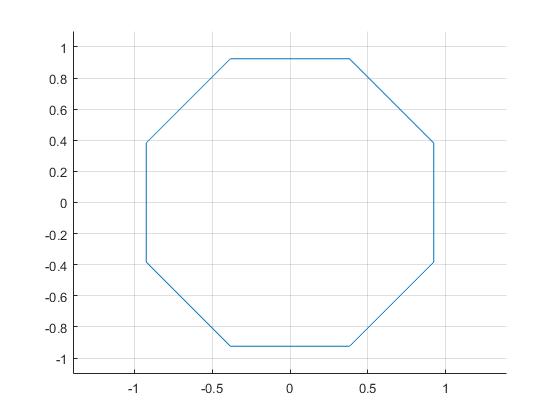
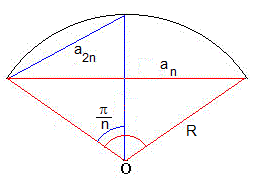
Calculamos la longitud del lado a_n un polígono regular de n lados inscrito en la circunferencia de radio R, (en color rojo).

${\displaystyle a_n=2R\sin \left(\frac{\pi }{n}\right)}$

Del mismo modo, obtenemos la longitud del lado de un polígono regular inscrito de 2n lados (en color azul)

${\displaystyle a_{2n}=2R\sin \left(\frac{\pi }{2n}\right)}$

Teniendo en cuenta la relación trogonométrica

${\displaystyle \sin \left(\frac{\alpha }{2}\right)=\sqrt{\frac{1-\cos \alpha }{2}}=\sqrt{\frac{1-\sqrt{1-{\sin }^2\alpha }}{2}}}$

Establecemos la relación entre a_n y a_2n y por tanto, entre el perímetro P_n del polígono regular de n lados y el perímetro P_2n del polígono regular de 2n lados.

${\displaystyle P_{2n}=2nR\sqrt{2-\sqrt{4-\frac{P_n^2}{R^2{n}^2}}}}$

Tomando R=1, empezamos con el cuadrado

${\displaystyle \begin{array}{l}{P}_4=4\sqrt{2}\\ P_8=2·4\sqrt{2-\sqrt{4-\frac{4^2{\left(\sqrt{2}\right)}^2}{4^2}}}=2^3\sqrt{2-\sqrt{2}}\\ P_{16}=2·8\sqrt{2-\sqrt{4-\frac{8^2{\left(2-\sqrt{2}\right)}^2}{8^2}}}=2^4\sqrt{2-\sqrt{2+\sqrt{2}}}\\ P_{32}=2·16\sqrt{2-\sqrt{4-\frac{{16}^2{\left(\sqrt{2-\sqrt{2+\sqrt{2}}}\right)}^2}{{16}^2}}}=2^5\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2}}}}\\ \mathrm{....}\end{array}}$

Definimos la función auxiliar recursiva calculo_pi que calcula la parte

${\displaystyle \sqrt{2+\sqrt{2+\sqrt{2+\mathrm{...}}}}}$

function z = calculo_pi(n)
    if n>0
        z=sqrt(2+calculo_pi(n-1));
    else
        z=0;
    end
end

En el script, calculamos el resto del perímetro dividido entre dos y lo comparamos con el número π

format long
for n=1:10
    z=2^n*sqrt(2-calculo_pi(n-1));
end
disp([z; pi])

3.141591421504635
3.141592653589793